
Review the focus of the learning so far: We have been finding fractions of whole numbers and finding fractions of fractions of an area. Have students pair share and check their results.Highlight the importance of their writing realistic stories for each. Explain that they can refer to the fraction wall or use the paper strips and scissors to complete it. Have students find one half on the fraction wall and look for the subdivision of one half into thirds, identifying that one sixth is one third of one half.ĭistribute and discuss Attachment 1. Pose the question: What is one third of one half? Give students time to become familiar with the fraction strips reading the unit fractions shown and talking about the subdivisions that they see. Distribute Fraction Strips ( Material Master 7-7) to the students to supplement the paper strips.Have students share what they did and discuss the results. Pose another problem: Use the materials to show three quarters of one half. Pose the problem: Can you use the materials to show one half of one half. Provide pairs of students with strips of paper and coloured pens.Will the result be larger or smaller than both fractions?ĭiscuss. Ask: What if you find a fraction of a fraction.Remind the students that they have been finding fractions of whole numbers. Have individual students come and record their results on the class chart and explain their solutions on behalf of their group. Roly’s class: 3/5 of something is 18 so 2/5 is: Jo’s class: 3/5 of something is 15 so 5/5 is: Have the students pair share their solutions. How many students are in Jo’s class?ġ8 students in Roly’s class are on the mat. Is she right?ġ5 students in Jo’s class were sitting on the mat. She was asked how many would be in her team if it included 1/3 of the class. Have the students discuss in pairs the solutions to each: Begin this session by posing these three problems.Solve problems involving finding a fraction of a fraction, using a regional model.Record in words the actions and results of finding a fraction of a fraction.Recognise that a fraction of a fraction results in a smaller part.Review finding a fraction of a whole number.Whilst the games are introduced and used within sessions to consolidate ideas, they can also be added to the class or group independent activities, or be sent home for family challenges and enjoyment. These ideas are presented in five sessions however, as they include complex concepts that are fundamental to a student’s success with fractions, these sessions can be extended over a longer period of time. Having students respond to these, and create context of their own, will help them recognise the practical application of fraction multiplication.

Using realistic contexts for finding fractions of fractions is important. 3/4 of 2/3), focuses the students on recording and calculations as they explore the relationships between the numbers. Once this is clearly understood, working with unit parts that involve subdivision (eg.

1/3 of 3/8), establishes the conceptual understanding of the multiplication operation with fractions. The use an array model to visualise and solve problems involving finding a fraction of a fraction, by breaking an area into parts, horizontally and vertically, scaffolds the move from a whole number understanding to a fractional one.īeginning with problems that involve working with unit parts without subdivision (eg. In multiplying fractions students come to recognise that the language of ‘times’ and ‘of’ are interchangeable. Thirdly, by understanding the commutative property, students can make problems simpler by changing the order of the factors. Multiplying fractions requires a conceptual shift for the students who must clearly understand they are finding a part of a part. In multiplying whole numbers, students expect a product that is larger than either factor. The second is that when two fractions less than one are multiplied, the product is always less than either factor. For example, 1/2 x 1/4 is interpreted as 1/2 of 1/4. The first is that multiplying two fractions involves finding the fraction of another fraction. There are three key understandings that underpin multiplication of fractions. Having a sound knowledge of basic multiplication and division facts is fundamental to the students’ success in working with and understanding equivalent fractions, and, in this unit, multiplying fractions.
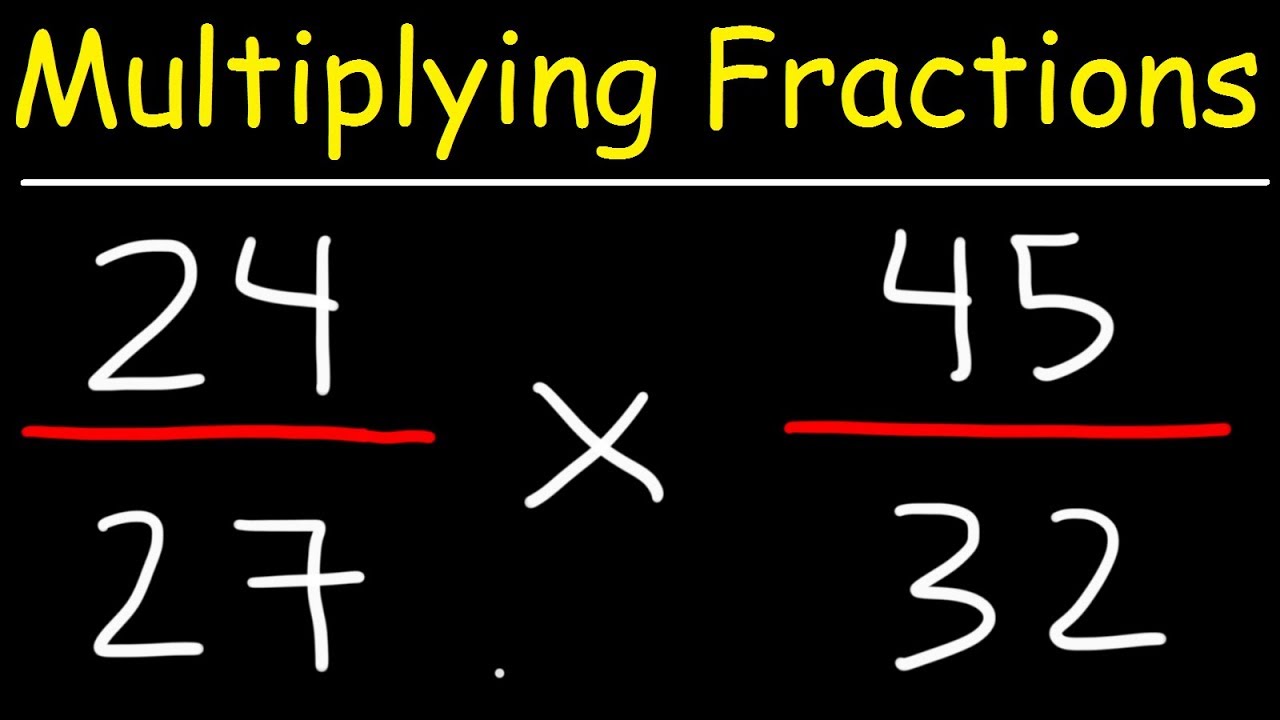
As in earlier units of work, an emphasis is given to having students model operations with fractions, using a range of materials and record using words and symbols.
#HOW TO MULTIPLY FRACTIONS SERIES#
This series of lessons builds upon students’ understanding and use of equivalent fractions as they solve fraction addition and subtraction problems.


 0 kommentar(er)
0 kommentar(er)
